1. 如圖,已知$AB= AC,AD= AE,AF⊥BC$于點(diǎn)F,則圖中全等三角形共有(
D
)
A.1對
B.2對
C.3對
D.4對
答案:D
解析:
1. $\triangle ABD \cong \triangle ACE$(SAS:$AB=AC$���,$\angle BAD=\angle CAE$����,$AD=AE$)
2. $\triangle ABF \cong \triangle ACF$(HL:$AF=AF$,$AB=AC$)
3. $\triangle ADF \cong \triangle AEF$(HL:$AF=AF$�,$AD=AE$)
4. $\triangle BDF \cong \triangle CEF$(SAS:$BD=CE$,$\angle BFD=\angle CFE$��,$DF=EF$)
D
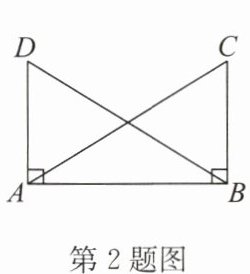
2. 如圖,$DA⊥AB,CB⊥AB$,垂足分別為A,B,$BD= AC$.根據(jù)這些條件不能推出的結(jié)論是(
C
)
A.$AD// BC$
B.$AD= BC$
C.AC平分$∠DAB$
D.$∠C= ∠D$
答案:C
解析:
∵DA⊥AB���,CB⊥AB�����,
∴∠DAB=∠CBA=90°��,AD//BC(A正確)�����。
在Rt△DAB和Rt△CBA中���,BD=AC,AB=BA�����,
∴Rt△DAB≌Rt△CBA(HL)���,
∴AD=BC(B正確)�����,∠D=∠C(D正確)����。
無法推出AC平分∠DAB����。
結(jié)論:C
3. 如圖,已知$∠A= ∠D= 90^{\circ }$,要用“HL”證明$△ABC\cong △DCB$,應(yīng)添加條件:
AB=DC(或AC=DB)
;要用“AAS”證明$△ABC\cong △DCB$,應(yīng)添加條件:
∠ACB=∠DBC(或∠ABC=∠DCB)
.
答案:AB=DC(或AC=DB) ∠ACB=∠DBC(或∠ABC=∠DCB)
解析:
要用“HL”證明$△ABC\cong △DCB$�����,應(yīng)添加條件:$AB=DC$(或$AC=DB$)���;要用“AAS”證明$△ABC\cong △DCB$,應(yīng)添加條件:$∠ACB=∠DBC$(或$∠ABC=∠DCB$)
4. 如圖,$AB⊥BC,AD⊥DC$,垂足分別為B,D,只需添加一個條件即可證明$△ABC\cong △ADC$,這個條件可以是
AB=AD(答案不唯一)
.(寫出一個即可)
答案:AB=AD(答案不唯一)
5. 如圖,$AB= CD,AE⊥BC,DF⊥BC$,垂足分別為E,F,$CE= BF$.求證:$AE= DF$.

答案:證明:
∵AE⊥BC,DF⊥BC,
∴∠DFC=∠AEB=90°,又
∵CE=BF,
∴CE?EF=BF?EF,即CF=BE.在Rt△DFC和Rt△AEB中,{CD=BA,CF=BE,
∴Rt△DFC≌Rt△AEB(HL),
∴AE=DF.
6. 如圖,點(diǎn)D在BC上,$DE⊥AB$于點(diǎn)E,$DF⊥BC$交AC于點(diǎn)F,$BD= CF,BE= CD$.若$∠AFD= 145^{\circ }$,則$∠EDF= $
55
$^{\circ }$.
答案:55
解析:
∵DE⊥AB�,DF⊥BC,
∴∠BED=∠CDF=90°.
在Rt△BDE和Rt△CFD中���,
$\left\{\begin{array}{l} BD=CF\\ BE=CD\end{array}\right.$���,
∴Rt△BDE≌Rt△CFD(HL),
∴∠BDE=∠CFD.
∵∠AFD=145°��,∠AFD+∠CFD=180°���,
∴∠CFD=180°-145°=35°����,
∴∠BDE=35°.
∵∠EDF+∠BDE=90°��,
∴∠EDF=90°-35°=55°.
55
7. 如圖,在$△ABC$中,$∠A= 90^{\circ }$,D為BC上一點(diǎn),$AB= BD$,過點(diǎn)D作$ED⊥BC$,交AC于點(diǎn)E,若$AC= 8,CD= 4$,則$△CDE$的周長是____
12
.
答案:12
解析:
連接BE���。
在$Rt△ABE$和$Rt△DBE$中���,
$\left\{\begin{array}{l} AB=BD\\ BE=BE\end{array}\right.$
$\therefore Rt△ABE\cong Rt△DBE(HL)$
$\therefore AE=DE$
$△CDE$的周長$=DE+EC+CD=AE+EC+CD=AC+CD$
$\because AC=8,CD=4$
$\therefore △CDE$的周長$=8+4=12$
12
8. 有下列結(jié)論:①一銳角和斜邊對應(yīng)相等的兩個直角三角形全等;②一銳角和一直角邊對應(yīng)相等的兩個直角三角形全等;③兩個銳角對應(yīng)相等的兩個直角三角形全等;④有一條直角邊和斜邊上的高對應(yīng)相等的兩個直角三角形全等.其中正確的是
①②④
.(填序號)
答案:①②④
9. 如圖,$CA⊥BC$,垂足為C,$AC= 2cm,BC= 6cm$,射線$BM⊥BQ$,垂足為B,動點(diǎn)P從點(diǎn)C出發(fā)以2 cm/s的速度沿射線CQ運(yùn)動,點(diǎn)N在射線BM上,隨著點(diǎn)P的運(yùn)動而運(yùn)動,滿足$PN= AB$,當(dāng)點(diǎn)P運(yùn)動
0或2或4或6
s時,$△BCA$與以點(diǎn)P,N,B為頂點(diǎn)的三角形全等.

答案:0或2或4或6