10. 陳老師設(shè)計(jì)了接力游戲,規(guī)則是:每人只能看到前一人給的式子,并進(jìn)行相應(yīng)計(jì)算,再將結(jié)果傳遞給下一人,若結(jié)果已是最簡,游戲結(jié)束.過程如圖所示.
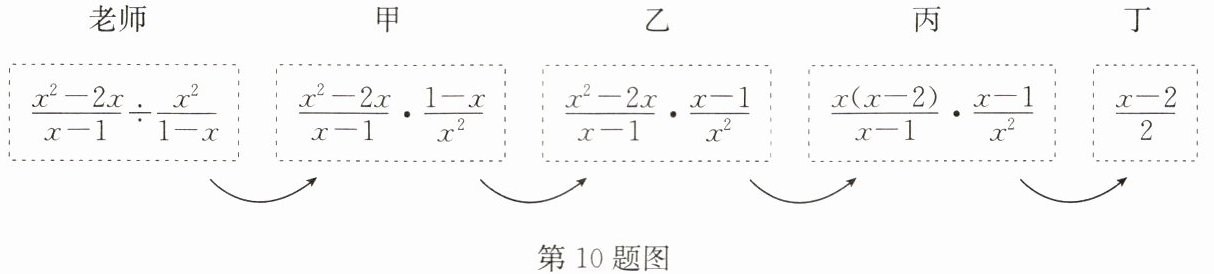
整個(gè)游戲過程,
乙����、丁
負(fù)責(zé)的那一步出現(xiàn)了錯(cuò)誤.
答案:乙�、丁
11. 計(jì)算:
(1)$\frac {m^{2}-2m+1}{1+4m+4m^{2}}÷\frac {2-2m}{2m+1}$; (2)$\frac {a^{2}-3a}{a^{2}+a}÷\frac {a-3}{a^{2}-1}\cdot \frac {a+1}{a-1}$.
答案:解:
(1)原式$=\frac {(m-1)^{2}}{(1+4m+4m^{2})}÷\frac {2-2m}{2m+1}=\frac {(m-1)^{2}}{(1+2m)^{2}}\cdot \frac {2m+1}{-2(m-1)}=-\frac {m-1}{2(1+2m)}=\frac {1-m}{2+4m}.$
(2)原式$=\frac {a(a-3)}{a(a+1)}÷\frac {a-3}{a^{2}-1}\cdot \frac {a+1}{a-1}=\frac {a(a-3)}{a(a+1)}\cdot \frac {(a+1)(a-1)}{a-3}\cdot \frac {a+1}{a-1}=a+1.$
12. (1)先化簡,再求值:$\frac {x^{2}-9}{x^{2}+6x+9}\cdot \frac {3x^{3}+9x^{2}}{x^{2}-3x}$,其中$x= -\frac {1}{3}$;
(2)已知$\frac {a}{2}= \frac ����{3}≠0$,求代數(shù)式$\frac {5a-2b}{a^{2}-4b^{2}}\cdot (a-2b)$的值.
答案:解:
(1)原式$=\frac {(x+3)(x-3)}{(x+3)^{2}}\cdot \frac {3x^{3}+9x^{2}}{x^{2}-3x}=\frac {(x+3)(x-3)}{(x+3)^{2}}\cdot \frac {3x^{2}(x+3)}{x(x-3)}=3x.$當(dāng)$x=-\frac {1}{3}$時(shí),原式$=3×(-\frac {1}{3})=-1.$
(2)原式$=\frac {5a-2b}{a^{2}-4b^{2}}\cdot (a-2b)=\frac {5a-2b}{(a+2b)(a-2b)}\cdot (a-2b)=\frac {5a-2b}{a+2b}.$$\because \frac {a}{2}=\frac {3}≠0,\therefore a=\frac {2}{3}b.$把$a=\frac {2}{3}b$代入,原式$=\frac {5×\frac {2}{3}b-2b}{\frac {2}{3}b+2b}=\frac {1}{2}.$
13. (2024春·杭州月考)老師在黑板上書寫了一道題目的正確計(jì)算過程,隨后用手遮住了其中一部分,如圖所示:

(1)求被手遮住部分的代數(shù)式;
(2)等式左邊代數(shù)式的值能等于0嗎? 請說明理由.
答案:解:
(1)設(shè)被手遮住部分的代數(shù)式為A,則$A=\frac {x+1}{x-1}\cdot \frac {x}{x+1}÷\frac {x^{2}-1}{x^{2}-2x+1}=\frac {x}{x-1}\cdot \frac {(x-1)^{2}}{(x+1)(x-1)}=\frac {x}{x+1}.$
(2)等式左邊代數(shù)式的值不能等于0.理由如下:若等式左邊代數(shù)式的值為0,則$\frac {x+1}{x-1}=0$,即$x+1=0,$解得$x=-1,$當(dāng)$x=-1$時(shí),$x+1=0$,分式無意義,
∴等式左邊代數(shù)式的值不能等于0.
14. 先化簡$(xy^{2}+x^{2}y)\cdot \frac {x}{x^{2}+2xy+y^{2}}÷\frac {2xy}{x^{2}-y^{2}}$,再選取一組你喜愛的$x,y$的值代入求值.
答案:解:原式$=xy(x+y)\cdot \frac {x}{x^{2}+2xy+y^{2}}÷\frac {2xy}{x^{2}-y^{2}}=xy(x+y)\cdot \frac {x}{(x+y)^{2}}\cdot \frac {(x+y)(x-y)}{2xy}=\frac {x(x-y)}{2}=\frac {x^{2}-xy}{2}.$$\because xy≠0,x+y≠0,x-y≠0,$
∴當(dāng)$x=2,y=1$時(shí),原式=1.(x,y的取值不唯一)