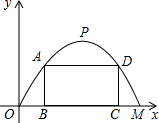
$解???:(1)M(12�,0),??????P(6�����,6)???$
$???(2)∵???頂點(diǎn)坐標(biāo)???(6��,6)???$
$∴設(shè)???y=a(x-6)^2+6(a\neq 0)???$
$又∵圖象經(jīng)過???(0�,0)???$
$???∴0=a(0-6)^2+6???$
$???∴a=-\frac {1}{6}???$
$∴這條拋物線的函數(shù)解析式為???y=-\frac {1}{6}(x-6)^2+6,???$
$即???y=-\frac {1}{6}x^2+2x.???$
(3)設(shè)A(x,y)
$???∴A(x��,??????-\frac {1}{6}(x-6)^2+6)???$
$∵四邊形???ABCD???是矩形���,$
$???∴AB=DC=-\frac {1}{6}(x-6)^2+6���,???$
$根據(jù)拋物線的軸對稱性,可得:???OB=CM=x�����,???$
$???∴BC=12-2x,???即???AD=12-2x����,???$
$∴令???L=AB+AD+DC=2[-\frac {1}{6}(x-6)^2+6]+12-2x=-\frac {1}{3}x^2+2x+12???$
$???=-\frac {1}{3}(x-3)^2+15.???$
$∴當(dāng)???x=3�,??????L???最大值為???15???$
$???∴AB、??????AD���、??????DC???的長度之和最大值為???15???米.$