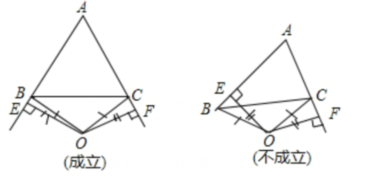
證明:?$(1) $?過點?$ O $?分別作?$ O E \perp A B $?于?$ E$?�����,
?$O F \perp A C $?于?$ F$?���,
由題意知,
在?$ R t \triangle O E B $?和?$ R t \triangle O F C $?中
?$\begin {cases}{O B=O C}\\{O E=O F}\end {cases}$?
∴?$R t \triangle O E B \cong R t \triangle O F C(H L)$?,
∴?$∠A B C=∠A C B$?�����,
∴?$A B=A C $?����;
?$(2)$?過點?$ O $?分別作?$ O E \perp A B $?于?$ E$?,?$ O F \perp A C $?于?$ F$?����,
由題意知,?$ O E=O F $?����,?$∠B E O=∠C F O=90°$?
∵在?$ Rt \triangle O E B $?和?$Rt \triangle O F C $?中
?$\begin {cases}{O B=O C}\\{O E=O F}\end {cases}$?
∴?$Rt \triangle O E B \cong R t \triangle O F C(H L)$?,
∴?$∠O B E=∠O C F$?�����,
又 ∵?$O B=O C$?�,
∴?$∠O B C=∠O C B$?��,
∴?$∠A B C=∠A C B$?��,
∴?$A B=A C $?;
?$(3)$?不一定成立����,?$ $?當(dāng)?$ ∠A $?的平分線所在直線與邊?$ B C$?
的垂直平分線重合時?$ A B=A C$?,?$ $?否則?$ A B \neq A C.$