電子課本網(wǎng) › 第44頁

第44頁

信息發(fā)布者：

C

3

2

$解：設(shè)點(diǎn)C到AB的距離為d$

$∴ \frac 12×AC×BC=\frac 12×AB×d$

$∴ d=\frac {12}5\ \mathrm {cm}$

$(1)d>2\ \mathrm {cm}$

$∴直線AB與圓C相離$

$(2)若直線AB與圓C相切，則 r=d=\frac {12}5\ \mathrm {cm}$

$(3)若相切，則 r=\frac {12}5\ \mathrm {cm}$

$若點(diǎn)A在內(nèi)部，點(diǎn)B在圓上或在圓的外部，則 3\ \mathrm {cm}＜r≤4\ \mathrm {cm}$

$ 綜上得 r=\frac {12}5\ \mathrm {cm}或3\ \mathrm {cm}＜r≤4\ \mathrm {cm}.$

$解：(1)如圖，當(dāng)點(diǎn)O向左移動(dòng)1\ \mathrm {cm}時(shí)，PO′=PO-O′O=3-1=2(\ \mathrm {cm})，$

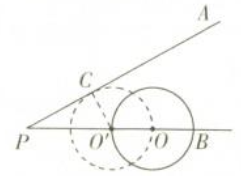
$作O′C⊥PA于C，$

$∵∠P=30°，$

$∴O′C=\frac {1}{2}PO′=1(\ \mathrm {cm}).$

$∵圓的半徑為1\ \mathrm {cm}，$

$∴⊙O與直線PA的位置關(guān)系是相切.$

$(2)如圖：當(dāng)點(diǎn)O由O′向左繼續(xù)移動(dòng)時(shí)，PA與圓相交，當(dāng)移動(dòng)到O″時(shí)，相切，$

$ 此時(shí)O″P=PO′=2(\ \mathrm {cm}).$

$∵OP=3\ \mathrm {cm}，$

$∴OO′=1\ \mathrm {cm}，$

$∴OO″=OP+O″P=3+2=5，$

$ ∴點(diǎn)O移動(dòng)的距離d的范圍滿足1\ \mathrm {cm}＜d＜5\ \mathrm {cm}時(shí)相交.$

亚洲激情+欧美激情,无码任你躁久久久久久,我的极品美女老婆,性欧美牲交在线视频,亚洲av高清在线一区二区三区