解:?$(2)$?在?$PC$?上截取?$PD=AP,$?連接?$AD�,$?如圖?$1:$?
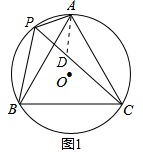
∵∠APC=60°,
?$∴△APD$?是等邊三角形����,
?$∴AD=AP=PD,$??$∠ADP=60°�����,$??$∠ADC=120°.$?
?$∵∠APB=∠APC+∠BPC=120°,$?
?$∴∠ADC=∠APB.$?
在?$△APB$?和?$△ADC$?中��,?$∠APB=∠ADC�,$??$∠ABP=∠ACD,$??$AP=AD�,$?
?$∴△APB≌△ADC,$?
?$∴BP=CD.$?
又?$∵PD=AP�,$?
?$∴PC=PA+PB.$?
?$(3)$?當(dāng)點(diǎn)?$P$?為?$\widehat{AB}$?的中點(diǎn)時(shí),四邊形?$APBC$?的面積最大.
理由如下:如圖?$2��,$?過(guò)點(diǎn)?$P$?作?$PE⊥AB�����,$?垂足為?$E����,$?過(guò)點(diǎn)?$C$?作?$CF⊥AB����,$?垂足為?$F.$?
?$∵S_{△APB}=\frac {1}{2}AB·PE,$??$S_{△ABC}=\frac {1}{2}AB·CF�����,$?
?$∴S_{四邊形APBC}=\frac {1}{2}AB·(PE+CF).$?
當(dāng)點(diǎn)?$P$?為?$\widehat{AB}$?的中點(diǎn)時(shí),?$PE+CF=PC�,$??$PC$?為?$⊙O$?的直徑,
∴此時(shí)四邊形?$APBC$?的面積最大.
?$∵⊙O$?的半徑為?$1�,$?
∴其內(nèi)接正三角形的邊長(zhǎng)?$AB=\sqrt{3},$?
?$∴S_{四邊形APBC}=\frac {1}{2}×2×\sqrt{3}=\sqrt{3}.$?