亚洲激情+欧美激情,无码任你躁久久久久久,我的极品美女老婆,性欧美牲交在线视频,亚洲av高清在线一区二区三区

電子課本網(wǎng) › 第49頁(yè)

第49頁(yè)

信息發(fā)布者：
30°
?$(-\sqrt{3}，1)$?
40°
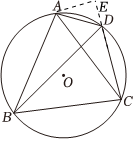
證明：?$(1)∵$?四邊形?$ABCD$?內(nèi)接于?$⊙O.$?
?$∴∠ABC+∠ADC=180°，$?
?$∵∠ABC=60°，$?
?$∴∠ADC=120°，$?
?$∵DB$?平分?$∠ADC，$?
?$∴∠ADB=∠CDB=60°，$?
?$∴∠ACB=∠ADB=60°，$??$∠BAC=∠CDB=60°，$?
?$∴∠ABC=∠BCA=∠BAC，$?
?$∴△ABC$?是等邊三角形.
?$(2)$?解：過(guò)點(diǎn)?$A$?作?$AE⊥CD$?于點(diǎn)?$E，$?
?$∴∠AED=90°，$?
∵四邊形?$ABCD$?為圓內(nèi)接四邊形，
?$∴∠ADC=180°-∠ABC=120°，$?

?$∴∠ADE=60°，$?
?$∴∠DAE=30°，$?
?$∴DE=\frac {1}{2}AD=1，$?
?$∴AE=\sqrt {AD^2-DE^2}=\sqrt {3}，$?
?$∵CD=3，$?
?$∴CE=CD+DE=3+1=4，$?
在?$Rt△AEC$?中，?$∠AED=90°，$?
?$∴AC=\sqrt {AE^2+CE^2}=\sqrt {19}，$?
?$∵△ABC$?是等邊三角形，
?$∴AB=BC=AC=\sqrt {19}，$?
?$∴△ABC$?的周長(zhǎng)為?$3\sqrt {19}.$?

證明：?$(1)∵∠BAC=∠ADB，$??$∠BAC=∠CDB，$?
?$∴∠ADB=∠CDB，$?
?$∴BD$?平分?$∠ADC，$?
?$∵BD$?平分?$∠ABC，$?
?$∴∠ABD=∠CBD，$?
∵四邊形?$ABCD$?是圓內(nèi)接四邊形，
?$∴∠ABC+∠ADC=180°，$?
?$∴∠ABD+∠CBD+∠ADB+∠CDB=180°，$?
?$∴2(∠ABD+∠ADB)=180°，$?
?$∴∠ABD+∠ADB=90°，$?
?$∴∠BAD=180°-90°=90°.$?
?$(2)$?解：?$∵∠BAE+∠DAE=90°，$??$∠BAE=∠ADE，$?
?$∴∠ADE+∠DAE=90°，$?
?$∴∠AED=90°，$?
?$∵∠BAD=90°，$?
?$∴BD$?是圓的直徑，
?$∴BD$?垂直平分?$AC，$?
?$∴AD=CD，$?
?$∵AC=AD，$?
?$∴△ACD$?是等邊三角形，
?$∴∠ADC=60°$?
?$∵BD⊥AC，$?
?$∴∠BDC=\frac {1}{2}∠ADC=30°，$?
?$∵CF∥AD，$?
?$∴∠F+∠BAD=90°，$?
?$∴∠F=90°，$?
∵四邊形?$ABCD$?是圓內(nèi)接四邊形，
?$∴∠ADC+∠ABC=180°，$?
?$∵∠FBC+∠ABC=180°，$?
?$∴∠FBC=∠ADC=60°，$?
?$∴BC=2BF=4，$?
?$∵∠BCD=90°，$??$∠BDC=30°，$?
?$∴BC=\frac {1}{2}BD，$?
?$∵BD$?是圓的直徑，
∴圓的半徑長(zhǎng)是?$4.$
?
上一頁(yè) 下一頁(yè)