?$(1)$?證明:∵四邊形?$ABCD$?是矩形
∴?$∠BAD=∠B=90°$?
由翻折可知�����,?$AF⊥DE$?
∴?$∠BAF+∠FAD=∠FAD+∠ADE=90°$?
∴?$∠ADE=∠BAF$?
∴?$△ABF∽△DAE$?
?$(2)$?解:如圖��,過點?$F$?作?$MN//BC$?交?$AB$?于?$M��,$?交?$CD$?于?$N$?
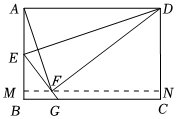
四邊形?$AMND$?是矩形�����,設(shè)?$EM=x$?
由翻折可知�����,?$AE=EF�,$??$AD=DF=3$?
∵點?$E$?是?$AB$?的中點,?$AB=2$?
∴?$AE=EF=1$?
∵?$∠BAD=∠EFD=90°��,$??$∠EMF=∠DNF=90°$?
∴?$∠EFM+∠DFN=90°�����,$??$∠DFN+∠FDN=90°$?
∴?$∠EFM=∠FDN$?
∴?$△EFM∽△FDN$?
∴?$\frac {EM}{FN}=\frac {FM}{DN}=\frac {EF}{FD}=\frac {1}{3}$?
∴?$FN=3EM=3x�����,$??$FM=3-3x$?
在?$Rt△EFM$?中���,?$EF=EA=1$?
?$x^2+(3-3x)^2=1^2$?
解得?$x_1=1($?舍去)�����,?$x_2=\frac {4}{5}$?
∴?$EM=\frac 45���,$??$FM=\frac {3}{5}$?
∵?$FM//BC$?
∴?$△EMF∽△EBG$?
∴?$\frac {EM}{EB}=\frac {FM}{BG}��,$?即?$\frac {\frac {4}{5}}{1}=\frac {\frac {3}{5}}{BF}$?
∴?$BG=\frac {3}{4}$?