亚洲激情+欧美激情,无码任你躁久久久久久,我的极品美女老婆,性欧美牲交在线视频,亚洲av高清在线一区二区三区

電子課本網(wǎng) › 第25頁

第25頁

信息發(fā)布者：
3
解：?$(1) $?由題意?$\begin{cases}{a-b+4=0}\\{16a+4b+4=0}\end{cases}，$?解得?$\begin{cases}{a=-1}\\{b=3 }\end{cases}$?
∴?$a=-1，$??$b=3$?
?$(2)$?由?$(1)$?可知拋物線對應的函數(shù)表達式為?$y=-x^2+3x+4$?
∵?$D$?是拋物線上的一點，且點?$D$?的橫坐標為?$1$?
∴?$y=-1+3+4=6$?
∴?$D(1，$??$6)$?
設直線?$AD$?的表達式為?$y=kx+m$?
∴?$\begin{cases}{k+m=0}\\{k+m=6}\end{cases}，$?解得?$\begin{cases}{k=3}\\{m=3}\end{cases}$?
∴直線?$AD$?的表達式為?$y=3x+3$?
設?$P(n，$??$3n+3)(-1< n< 1)，$?則?$H(n，$??$-n^2+3n+4)$?
∴?$PH=-n^2+3n+4-(3n+3)=-n^2+1$?
∴?$-n^2+1=\frac {1}{2}$?
解得?$n_{1}=\frac {\sqrt{2}}{2}，$??$n_{2}=-\frac {\sqrt{2}}{2}，$?均符合題意
∴點?$P $?的坐標為?$(\frac {\sqrt{2}}{2}，$??$ \frac {3\sqrt{2}}{2}+3 ) $?或?$(-\frac {\sqrt{2}}{2}，$??$- \frac {3\sqrt{2}}{2}+3)$?
解：?$(1)$?當?$x=800$?時，?$y=800×(50-30)=16000$?
∴當一次性銷售?$800$?千克時利潤為?$16000$?元
?$(2)$?設一次性銷售量在?$1000\sim 1750$?千克之間時，
每千克銷售利潤為?$50-30-0.01(x-1 000)=(-0.01x+30)$?元
∴?$y=x(-0.01x+30)=-0.01x^2+30x=-0.01(x^2-3000x)=-0.01(x-1500)^2+22500$?
∵?$-0.01< 0，$??$1000≤x≤1750$?
∴當?$x=1500$?時，?$y$?有最大值，最大值為?$22500$?
∴一次性銷售量在?$1000\sim 1750$?千克之間時的最大利潤為?$22500$?元
?$ (3)①$?當一次性銷售量在?$1000\sim 1750$?千克之間時，利潤為?$22100$?元
∴?$-0.01(x-1500)^2+22500=22100$?
解得?$x_{1}=1700，$??$x_{2}=1300$?
②當一次性銷售不低于?$1750$?千克時，均以某一固定價格銷售
設此時函數(shù)表達式為?$y=kx$?
由?$(2)$?知，當?$x=1750$?時，?$y=-0.01(1750-1500)^2+22500=21875$?
∴?$B(1750，$??$21875)$?
把點?$B$?的坐標代入表達式，得?$21875=1750k$?
解得?$k=12.5$?
∴當一次性銷售不低于?$1750$?千克時，函數(shù)表達式為?$y= 12.5x$?
當?$y=22100$?時，?$22100=12.5x，$?解得?$x=1768$?
綜上所述，當一次性銷售?$1300$?千克或?$1700$?千克或?$1768$?千克時，利潤為?$22100$?元 
解：?$(1)$?解方程?$x^2-6x+5=0$?得?$m=1，$??$n=5，$?則?$A(-1，$??$0)、$??$B(0，$??$5)$?
把?$A(-1，$??$0)、$??$B(0，$??$5)$?代入?$y=-x^2+bx+c $?
得?$ \begin{cases}{-1-b+c=0}\\{c=5}\end{cases}，$?解得?$\begin{cases}{b=4}\\{c=5}\end{cases}$?
∴拋物線對應的函數(shù)表達式為?$y=-x^2+4x+5 $?
?$(2)y=-x^2+4x+5=-(x-2)^2+9，$?則?$D(2，$??$9)$?
解方程?$-x^2+4x+5=0$?得?$x_{1}=-1，$??$x_{2}=5$?
則?$C(5，$??$0)$?
設直線?$BC$?對應的函數(shù)表達式為?$y=px+q$?
把?$C(5，$??$0)、$??$B(0，$??$5)$?代入，得?$ \begin{cases}{5p+q=0}\\{q=5}\end{cases}，$?解得?$\begin{cases}{p=-1}\\{q=5}\end{cases}$?
∴直線?$BC$?對應的函數(shù)表達式為?$y=-x+5$?
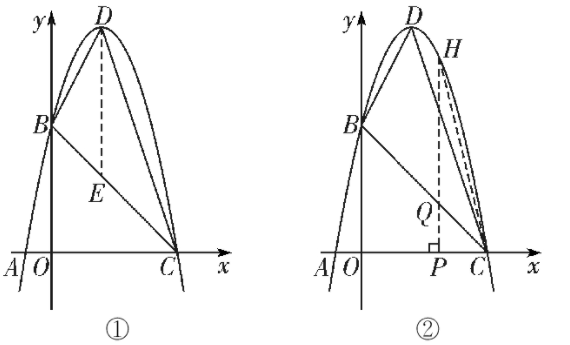
如圖①，作?$DE//y$?軸交?$BC$?于點?$E，$?則點?$E$?的坐標為?$(2，$??$3)$?
∴?$S_{△BCD}=S_{△BDE}+S_{△CDE}=\frac {1}{2} ×(9-3)×5=15$?
?$(3)$?如圖②，?$PH$?交?$BC$?于點?$Q$?
設?$P(t，$??$0)，$?則?$Q(t，$??$-t+5)，$??$H(t，$??$-t^2+4t+5)$?
∴?$PC=5-t，$??$QP=-t+5，$??$HQ=-t^2+4t+5-(-t+5)=-t^2+5t$?
若?$S_{△PCQ}∶S_{△HQC}=2∶3，$?則?$ \frac {\frac {1}{2} (5-t)(-t+5)}{\frac {1}{2}(5-t)(-t^2+5t)}=\frac {2}{3}$?
整理，得?$2t^2-13t+15=0$?
解得?$t_{1}=\frac {3}{2}，$??$t_{2}=5($?舍 去)
此時點?$P $?的坐標為?$(\frac 32，$??$0)$?
 若?$S_{△PCQ}∶S_{△HQC}=3∶2，$?則?$ \frac {\frac {1}{2} (5-t)(-t+5)}{\frac {1}{2} (5-t)(-t^2+5t)}=\frac {3}{2}$?
整理，得?$3t^2-17t+10=0$?
解得?$t_{1}=\frac {2}{3}，$??$t_{2}=5($?舍去)
此時點?$P $?的坐標為?$ (\frac {2}{3}，$??$0)$?
綜上所述，滿足條件的點?$P $?的坐標?$(\frac {2}{3} ，$??$0) $?或?$(\frac {3}{2}，$??$0 )$
?
上一頁 下一頁