解???$:(1)M(12��,0),$??????$P(6���,6)$???
???$(2)∵$???頂點(diǎn)坐標(biāo)???$(6,6)$???
∴設(shè)???$y=a(x-6)^2+6(a\neq 0)$???
又∵圖象經(jīng)過(guò)???$(0�,0)$???
???$∴0=a(0-6)^2+6$???
???$∴a=-\frac {1}{6}$???
∴這條拋物線的函數(shù)解析式為???$y=-\frac {1}{6}(x-6)^2+6,$???
即???$y=-\frac {1}{6}x^2+2x.$???
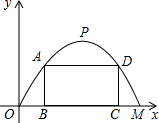
(3)設(shè)A(x,y)
???$∴A(x�����,$??????$-\frac {1}{6}(x-6)^2+6)$???
∵四邊形???$ABCD$???是矩形��,
???$∴AB=DC=-\frac {1}{6}(x-6)^2+6����,$???
根據(jù)拋物線的軸對(duì)稱(chēng)性,可得:???$OB=CM=x�����,$???
???$∴BC=12-2x���,$???即???$AD=12-2x�,$???
∴令???$L=AB+AD+DC=2[-\frac {1}{6}(x-6)^2+6]+12-2x=-\frac {1}{3}x^2+2x+12$???
???$=-\frac {1}{3}(x-3)^2+15.$???
∴當(dāng)???$x=3,$??????$L$???最大值為???$15$???
???$∴AB����、$??????$AD、$??????$DC$???的長(zhǎng)度之和最大值為???$15$???米.